Exercise Set 9 Answers

Find the first and second dervatives of the following expressions.
1. $y=3x^5+2x-1$
2. $y=4x^{-1}$
3. $y=x^{\frac{1}{2}}+x^{\frac{1}{3}}$
4. $y=x^7+\sin(x)$
5. $y=e^x+5$
Answers:
1. \[\begin{align*} y &= 3x^5 + 2x -1$\\ \frac{dy}{dx} &= 15x + 2\\ \frac{d^2y}{dx^2} &= 15 \end{align*}\]
2. \[\begin{align*} y&=4x^{-1}\\ \frac{dy}{dx} &= -4x^{-2}\\ \frac{d^2y}{dx^2} &= 8x^{-3} \end{align*}\]
3. \[\begin{align*} y &= x^\frac{1}{2} + x^\frac{1}{3}\\ \frac{dy}{dx} &= \frac{1}{2}x^{-\frac{1}{2}} + \frac{1}{3}x^{-\frac{2}{3}}\\ \frac{d^2y}{dx^2} &= -\frac{1}{4}x^{-\frac{3}{2}} + -\frac{2}{9}x^{-\frac{5}{3}} \end{align*}\]
4. \[\begin{align*} y &= x^6 \sin(x)\\ \frac{dy}{dx} &= 7x^6 + \cos (x)\\ \frac{d^2y}{dx^2} &= 42x^5 - \sin(x) \end{align*}\]
5. \[\begin{align*} y &= e^x + 5\\ \frac{dy}{dx} &= e^x\\ \frac{d^2y}{dx^2} &= e^x \end{align*}\]
Find the derivative of $(1+2x)(x-x^2)$ in two ways: first, expand and find the derivative; second, use the product rule. Your answers should agree!

Answer:

Method 1, expand and find the derivative: \[\begin{align*} y &= (1+2x)(x-x^2)\\ &=x - x^2 + 2x^2 - 2x^3\\ &=-2x^3 + x^2 + x\\ \frac{dy}{dx} &= -6x^2 + 2x + 1 \end{align*}\]

Method 2, product rule. Let $y=h(x) = f(x)g(x)$ where $f(x) = (1+2x)$ and $g(x) = (x-x^2)$ \[\begin{align*} y &= (1+2x)(x-x^2)\\ y' &= 2(x-x^2)+(1+2x)(1-2x)\\ &=-6x^2 + 2x + 1 \end{align*}\] And as expected, we have obtained the same answer with both methods.
Use the product rule to show that $(af)'(x)=af'(x)$ for any differentiable function $f$ and number $a$.

Answer:

We wish to show that $(af)'(x) = a f(x)$, or in Leibniz notation, $\frac{d}{dx}af(x)=a \frac{d}{dx}f(x)$. This can be shown using product rule, where one of the functions is $f(x)$ and the other is simply the constant function $g(x)=a$ \[\begin{align*} (gf)'(x) &= g(x)' f(x) + g(x)f'(x)\\ &= 0f(x)+g(x)f'(x)\\ &=a f'(x) \end{align*}\] or in Leibniz notation \[\begin{align*} \frac{d}{dx}(g(x)f(x))&=\frac{d}{dx}(g(x))f(x)+g(x)\frac{d}{dx}f(x)\\ &=0f(x)+g(x)\frac{d}{dx}f(x)\\ &=a\frac{d}{dx}f(x) \end{align*}\] using $g'(x)=\frac{d}{dx}g(x)=0$ because the derivative of a constant function is zero.
Use the chain rule to show that $(f(ax+b))'=af'(ax+b)$ for any differentiable function $f$ and numbers $a$ and $b$.

Answer:

To show $(f(ax+b))' = a f'(ax+b)$, we can recognise the derivative as an application of chain rule: $(f(g(x)))' = g'(x)f'(g(x))$, where $g(x) = ax+b$. Since $g'(x) = a$, we have that \[(f(ax+b))'= a (f'(ax+b))\]
Find the derivatives of the following functions (you may like to use the additional rules you have just derived in the previous two questions).
1. $f(x)=\sqrt{2}\sin(x)$
2. $f(x)=\ln(2)\ln(x)$
3. $f(x)=\cos(3x)$
4. $f(x)=\sin(5x+2)$
5. $f(x)=3e^{2x}$
6. $f(x)=3e^{2x+1}$
Answers:
1. \[f(x)= \sqrt{2} \sin (x)\\ f'(x) = \sqrt{2} \cos (x)\]
2. \[f(x) = \ln (2) \ln(x)\\ f'(x) = \frac{\ln 2}{x}\]
3. \[f(x) = \cos (3x)\\ f'(x) = -3 \sin (3x)\]
4. \[f(x) = \sin (5x+2)\\ f'(x) = 5 \cos (5x+2)\]
5. \[f(x) = 3e^{2x}\\ f'(x) = 6e^{2x}\]
6. \[f(x) = 3e^{2x+1}\\ f'(x) = 6e^{2x+1}\]
Find the derivatives of the following functions using the product rule.
1. $f(x)=3x^2\sin(x)$
2. $f(x)=\sin(x)\cos(x)$
3. $f(x)=(x^3-x)e^x$
4. $f(x)=x\ln(x)$
Answers:
1. \[f(x) = 3x^2 \sin (x)\\ f'(x) = 6x \sin(x) + 3x^2 \cos(x)\]
2. \[ f(x) = \sin(x)\cos(x) \quad(=\frac{1}{2}\sin(2x))\\ f'(x) = \cos^2(x) - \sin^2(x) = \cos(2x)\]
3. \[f(x) = (x^3 - x)e^x\\ f'(x) = (3x^2 - 1)e^x + (x^3 - x)e^x\\ = (x^3 + 3x^2 - x - 1)e^x\]
4. \[f(x) = x \ln (x)\\ f'(x) = \ln(x) + 1\]
Find the derivatives of the following functions using the chain rule.
1. $f(x)=\cos(x^2)$
2. $f(x)=\sin(\cos(x))$
3. $f(x)=e^{\sin(x)}$
4. $f(x)=\sin^{100}(x)$
Answers:

These are all applications of chain rule for taking derivatives of functions of the from $f(x) = h(g(x))$
1. This is a composition of two functions, $h(x) = \cos(x)$, $g(x) = x^2$ \[f'(x) = -2x \sin(x^2)\]
2. Taking the derivative of $h(g(x))$ where $h(x) = \sin(x)$ and $g(x) = \cos(x)$ \[f'(x) = -\sin(x)\cos(\cos(x))\]
3. $f'(x) = (h(g(x)))'$ where $h(x) = e^x$ and $g(x) = \sin(x)$ \[f'(x) = \cos(x)e^{\sin(x)}\]
4. Here, $h(x) = x^{100}$ and $g(x) = \sin(x)$ \[f'(x) = 100\cos(x)\sin^{99}(x)\]
Find the derivatives of the following functions using the quotient rule.
1. $f(x)=\dfrac{1}{1+x^2}$
2. $f(x)=\dfrac{x^2}{1+x^2}$
3. $f(x)=\dfrac{x^3}{e^{3x}}$
4. $f(x)=\dfrac{x-\sqrt{x}}{x^2}$
5. $f(x)=\dfrac{\sin(x)}{\cos(x)}$
Answers:
1. $f(x) = \frac{1}{1+x^2}$. Applying quotient rule: \[f'(x) = \frac{-2x}{(1+x^2)^2}\]
2. $f(x) = \frac{x^2}{1+x^2}$. \[f'(x) = \frac{2x(1+x^2) - x^2(2x)}{(1+x^2)^2} = \frac{2x}{(1+x^2)^2}\]
3. $f(x) = \frac{x^3}{e^{3x}}$ \[f'(x) = \frac{3x^2 \times e^{3x} - x^3\times 3e^{3x}}{e^{6x}} = \frac{3(x-1)x^2}{e^{3x}}\]
4. $f(x) = \frac{x-x^{\frac{1}{2}}}{x^2}$ \[f'(x) = \frac{(1-\frac{1}{2}x^{-\frac{1}{2}})\times x^2 - (x-x^\frac{1}{2})\times 2x}{x^4}\\ = \frac{x^2 - \frac{1}{2}x^{\frac{3}{2}} - 2x^2 + 2x^{\frac{3}{3}}}{x^4}\\ =\frac{-x^2 + \frac{3}{2}x^{\frac{3}{2}}}{x^4} = -x^{-2} + \frac{3}{2}x^{-\frac{5}{2}}\]
5. $f(x) = \frac{\sin(x)}{\cos{x}}$ \[f'(x) = \frac{\cos^2(x) + \sin^2(x)}{\cos^2 (x)} = \frac{1}{\cos^2(x)} = \sec^2(x)\]
Find the derivatives of the following functions.
1. $f(x)=\sin^2(\sin(x))$
2. $f(x)=\ln(x^2)$
3. $f(x)=a^x$ for any $a>0$
4. $f(x)=e^x\sin(x^2)$
Answers:
1. We recognise this as a composition of three functions $f(x)=s(t(u(x)))$ with $u(x)=\sin(x)$ $t(x)=\sin(x)$ $s(x)=x^2$ First applying the chain rule to $s$ and $t$ \[\frac{df(x)}{dx}=\frac{ds(t)}{dt}\frac{dt(u(x))}{dx}\] Then applying the chain rule to $t$ and $u$ \[\frac{df(x)}{dx}=\frac{ds(t)}{dt}\left(\frac{dt(u)}{du}\frac{du(x)}{dx}\right)\] so we have \[\frac{df(x)}{dx}=2\sin(\sin(x))\times \cos(\sin(x))\times\cos(x).\]
2. We could first turn the power into a product to obtain $f(x)=2\ln(x)$, then the derivative is \[\frac{df(x)}{dx}=2\frac{1}{x}.\]
  
  Alternatively, we could use the chain rule. Letting $u(x)=x^2$ we have \[\begin{align*} \frac{df(x)}{dx}&=\frac{\ln(u)}{du}\frac{du(x)}{dx}\\ &=\frac{1}{u}2x\\ &=\frac{2x}{x^2}\\ &=\frac{2}{x}. \end{align*}\]
3. We can use the natural logarithm to obtain \[f(x)=e^{\ln(a^x)}=e^{x\ln(a)}.\] Then \[\frac{df(x)}{dx}=\ln(a)e^{x\ln(a)}=\ln(a)e^{\ln(a^x)}=\ln(a)a^x.\]
4. We have $f(x)=s(x)t(u(x))$ with $s(x)=e^x$, $t(x)=\sin(x)$, $u(x)=x^2$. We have a product and a composition. First applying the product rule \[\frac{df(x)}{dx}=\frac{ds(x)}{dx}t(u(x))+s(x)\frac{dt(u(x))}{dx}.\] Then appying the chain rule \[ \frac{df(x)}{dx}=\frac{ds(x)}{dx}t(u(x))+s(x)\frac{dt(u)}{du}\frac{du(x)}{dx}.\] So, we have \[\begin{align*} \frac{df(x)}{dx}&=e^x\sin(x^2)+e^x\cos(x^2)2x\\ &=e^x(\sin(x^2)+2x\cos(x^2)) \end{align*}\]
Show that $\frac{d}{dx}\sinh(x)=\cosh(x)$ and $\frac{d}{dx}\cosh(x)=\sinh(x)$.

Answer:

$\dfrac{d}{dx}\sinh(ax)=\dfrac{d}{dx}\dfrac{e^{ax}-e^{-ax}}{2}=\dfrac{ae^{ax}-(-a)e^{-ax}}{2}=a\dfrac{e^{ax}+e^{-ax}}{2}=a\cosh(ax)$ and $\dfrac{d}{dx}\cosh(ax)=\dfrac{d}{dx}\dfrac{e^{ax}+e^{-ax}}{2}=\dfrac{ae^{ax}+(-a)e^{-ax}}{2}=a\dfrac{e^{ax}-e^{-ax}}{2}=a\sinh(ax)$.
Find all local maxima and minima of the following functions. Are there any global maxima or minima? Also sketch their graphs.
1. $f(x)=x^2+3x+1$
2. $f(x)=x^3-3x$
Answers:

For graph sketching we want to find the following:
- Where the curve crosses the $x$-axis and $y$-axis.
- The coordinates of any local maxima and minima.
- The general shape of the curve.
- Any asymptotes.
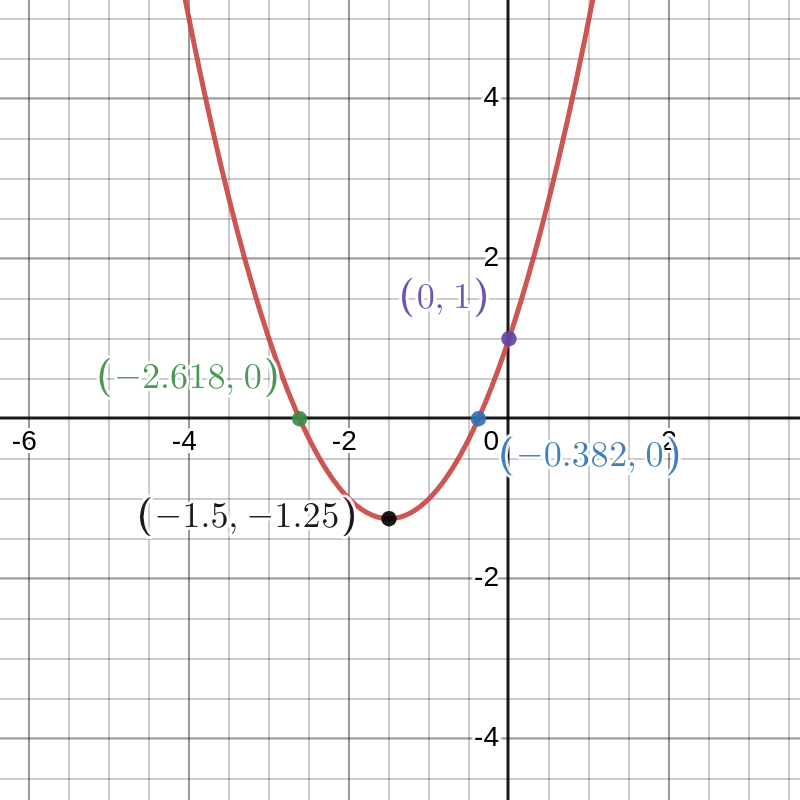
1. We have $f'(x)=2x+3$. Stationary points are where $f'(x)=0 \implies x=\frac{-3}{2}$.
  
  To check for local maxima and minima we find the second derivative: $f''(x)=2$. Since this is always postive, we only have one local minimum at $x=\frac{-3}{2}$, $y=-\frac{5}{4}$. From the dominant $x^2$ term being positive, we see this is a parabola which opens upwards, hence this minimum will be the global minimum and there are no local or global maxima.
  
  The curve crosses the $x$-axis where $f(x)=0$. Using the quadratic formula: \[x=\frac{-3\pm\sqrt{9-4}}{2}=\frac{-3\pm\sqrt{5}}{2}\] so the approximate solutions are $x_1=-2.618$ and $x_2=-0.382$.
  
  The curve crosses the $y$-axis at $f(0)=1$.
  
  Sketch:
2. We have $f'(x)=3x^2-3$. Stationary points are where $f'(x)=0 \implies x=\pm 1$.
  
  To check for local maxima and minima we find the second derivative: $f''(x)=6x$. This implies that $(-1,2)$ is a local maximum and $(1,-2)$ is a local minimum. From the dominant $x^3$ term, we see that $f(x)$ can take arbitrarily large positive and negative values, hence there are no global maxima or minima.
  
  The curve crosses the $x$-axis where $f(x)=0$. Factorising the cubic, we have: \[f(x)=x(x-\sqrt{3})(x+\sqrt{3})\] so the solutions are $x_0=0$ and approximately $x_1=-1.732$, $x_2=1.732$.
  
  The curve crosses the $y$-axis at $f(0)=0$.
  
  Sketch:
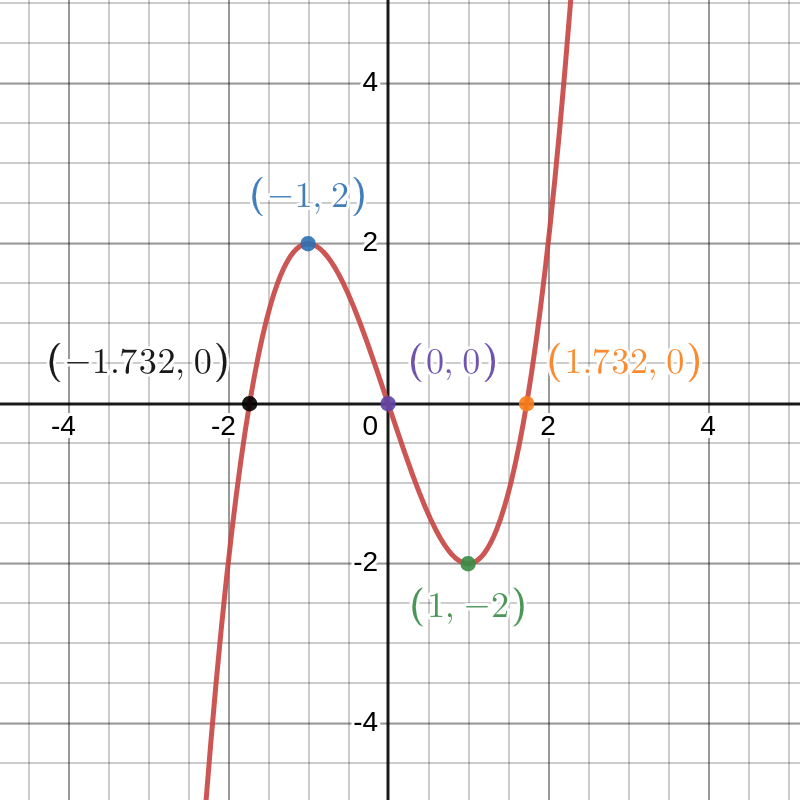
A particle moving in a straight line has displacement $x$ as a function of time $t\geq 0$ given by \[x=-t^{3}+5t^{2}+t.\]
1. Find the velocity $v$ and acceleration $a$.
2. What is the initial velocity?
3. What is the largest positive displacement?
4. At what time does the particle return to the origin?
Answers:
1. \[\begin{align*} x &= -t^3 + 5t^2 + t\\ v &= \frac{dx}{dt} = -3t^2 + 10t + 1\\ a &= \frac{dv}{dt} = \frac{d^2x}{dt^2} = -6t + 10 \end{align*}\]
2. $v(0) = 1$
3. To find the largest positive displacement, we must find the turning points of $x$. These times are found by solving for $v(t) = 0$ \[v = -3t^2 + 10t + 1 = 0\\ \text{solved by } t = \frac{5}{3}\pm \frac{2\sqrt{7}}{3}\] The solution $\frac{5}{3}-\frac{2\sqrt{7}}{3}$ is in negative time, and the shape of the dominant $-t^3$ term in $x$ suggests that the maximum will be at time $\frac{5}{3}+\frac{2\sqrt{7}}{3}$, but it is prudent to check the second derivative of $x$ (which is $a$). \[a(\frac{5}{3}-\frac{2\sqrt{7}}{3}) = 4\sqrt{7}\\ a(\frac{5}{3}+\frac{2\sqrt{7}}{3}) = -4\sqrt{7}\] And hence the maximum displacement does indeed occur at time $t=\frac{5}{3}+\frac{2\sqrt{7}}{3}$, and $x(\frac{5}{3}+\frac{2\sqrt{7}}{3}) \approx 21.9$
4. To find when the particle returns to the origin, we must solve for $x(t) = 0$. \[-t^3 + 5t^2 + t = 0\\ -t^2 + 5t + 1 = 0\\ t = \frac{5 \pm \sqrt{29}}{2}\] Where one solution is for a negative $t$, so the particle returns to the origin at $t = \frac{5 +\sqrt{29}}{2} \approx 5.19$
Find the points of inflection of the following functions.
1. $f(x)=\dfrac{x^3}{3}-\dfrac{x^2}{2}-2x+5$
2. $f(x)=x+\sin(x)$
Answer:
1. To find points of inflection, we find the points at which the second derivative is zero and the third derivative is non-zero. \[f(x) = \frac{x^3}{3} - \frac{x^2}{2} - 2x + 5\\ f'(x) = x^2 - x - 2\\ f'(x) = 0 = x^2 - x- 2 = (x+1)(x-2)\\ f''(x) = 2x-1\\ f'''(x)=2\] The second derivative is zero at $x=\frac{1}{2}$, and the second derivative also changes signs either side of this point. Alternatively we simply note that $f''(x=\frac{1}{2}) = 0$ and $f'''(x=\frac{1}{2})\neq 0$, so it is an inflection point by the Third Derivative Test for Inflection Points.
2. \[f(x) = \sin (x) + x\\ f'(x) = \cos(x)+1\] So there are stationary points at $x = \frac{\pi}{2} + 2\pi k$ for any integer $k$. $f''(x) = -\sin(x)$, which is zero whenever $x = k\pi$ for integer $k$. The third derivative, $f'''(x) = -\cos(x)$ is non zero whenever $x \neq \frac{\pi}{2} + 2\pi k$. So the points of inflection, by the Third Derivative Test, are whenever $x=2\pi k$ for integer $k$. Note that half of these are also stationary points.
A rectangular box with no lid is made from a thin sheet of metal. The base is $2x\text{ mm}$ long and $x\text{ mm}$ wide, and the volume is $48000\text{ mm}^3$. Show that the area $A$ of metal used is given by \[A=2x^2+144000x^{-1} \text{ mm}^2.\] Find the value of $x$ for which the minimum area of metal is used along with the value of the minimum area.

Answer:

The volume of the box is given by $2x\times x \times h = 48000\text{ mm}^3$. We write the height in terms of volume and base area: $h = \frac{48000}{2x^2}$ The area of metal used is given by \[A = 2x^2 + 2\times 2x\times \frac{48000}{x^2} + 2 \times x \times \frac{48000}{2x^2}\\ =2x^2 + \frac{96000}{x} + \frac{48000}{x}\\ = 2x^2 + \frac{144000}{x}\] We wish to minimise the area of metal used to create the appropriate volume of box. This requires finding the minimum of the Area function. \[A' = 4x - \frac{144000}{x^2}\\ A' = 0 \Rightarrow 4x^3 = 144000\\ \Rightarrow x = 33.019mm\] We check this is a minimum by looking at the second derivative \[A''=4+\frac{288000}{x^3}\] which is positive for any postive $x$ value, hence we do have a minimum by the second derivative test. The corresponding area is \[ A= 6541.63\text{mm}^3.\]