Exercise Set 4

These exercises cover the topic of Trigonometry.

Tip: always start by drawing a labelled diagram in trigonometry questions.

1. Consider the smaller of the two angles between the hour hand and minute hand of a clock (remembering that the hour hand moves continuously!). Write the angles at the following times in both degrees and radians (in terms of $\pi$).

   1. 6:00
   2. 3:00
   3. 4:00
   4. 4:30
   5. 6:45

2. Convert the following angles from degrees to radians. Give answers both in terms of $\pi$ and to 2 d.p.

   1. $330^\circ$
   2. $22.5^\circ$
   3. $27^\circ$
   4. $35^\circ$

3. A bearing is the angle measured clockwise from North to the direction of interest (note how this differs to how we measure angles in the coordinate plane). A point $K$ is 12km due west of a second point $L$ and 25km due south of a third point $M$. Calculate the bearing of $L$ from $M$ (in degrees).

4. Solve (i.e. find all unknown angles and side lengths) the triangle $ABC$ where $A = 53^\circ$, $B = 61^\circ$ and $a = 12.6$cm.

5. Solve (i.e. find all unknown angles and side lengths) the triangle $ABC$ where $a=10.2$m, $c=14.6$m and $C = 32.5^\circ$.

6. Let $AOB$ be a triangle. $OA = 60$mm, $AB = 180$mm and $OB = 200$mm. Find angle $A$.

7. An angle of elevation is an angle that an imaginary straight line must be raised from the horizontal ground to line up with a point of interest above the ground. An observer is standing at a point $M$ which is $30$m from the base of a tower. On top of the tower is a vertical mast. If the angles of elevation of the top of the tower and the top of the mast from $M$ are $40^\circ$ and $50^\circ$ respectively, calculate the height of the mast.

8. The small hand of a clock is 75% the length of the long hand, which has length $x$. Calculate the distance between the ends of the hands at 5 o’clock (in terms of $x$).

9. A student $1.8$m tall is standing $24$m away from a tree and using a eye level instrument to measure the angle of elevation. The angle measured to the top of the tree is $12^\circ 34'$, calculate the height of the tree. (Degrees can be further subdivided in to minutes denoted $x'$ and seconds denoted $x''$, with $1'$ being $1/60$ of a degree and $1''$ being $1/60$ of a minute. To use a calculator you will first need to convert minutes and seconds to decimals.)

10. The angles of elevation of a navigation balloon that is flying in between two points on the ground $A$ and $B$ are $48^\circ$ and $62^\circ$ respectively. If $A$ and $B$ are $0.3$km apart, calculate the height of the balloon.

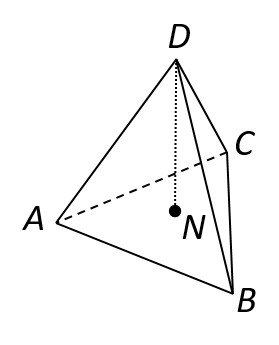
11. The figure below shows a tetrahedron with an equilateral triangle of side 2m forming the base and isosceles triangles of equal side 3m forming the slanting faces. Calculate:

    1. The height of the tetrahedron $ND$;
    2. The angle that edge $DA$ makes with the plane $ABC$;
    3. The angle between the planes $ACD$ and $ACB$.

1. This is a harder question using trigonometric identities. Here we shall derive a special (slightly simpler) case of the sum of two sinusoidal waves of the same frequency that was shown in lectures. We will consider two waves of the form $$y_1=A_1\sin(\omega t),\qquad y_2=A_2\cos(\omega t)$$ .
   1. First assume we can write $y_1+y_2$ in the form $A\sin(\omega t+\phi)$. Then using the trigonometric identity $$\sin(\theta+\phi)=\sin(\theta)\cos(\phi)+\cos(\theta)\sin(\phi)$$ deduce that $A_1=A\cos(\phi)$ and $A_2=A\sin(\phi)$.
   2. Now using the trigonometric identity $\sin^2(\theta)+\cos^2(\theta)=1$ show that $A^2=A_1^2+A_2^2$.
   3. Finally, using $\tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$, show that $\tan(\phi)=\frac{A_2}{A_1}$.
2. Using the formulas derived in the previous question for $A$ and $\phi$, write the following in the form $A\sin(\omega t + \phi)$.
   1. $-2\sin(\omega t) + 5\cos(\omega t)$
   2. $-5\cos(\omega t) + 5 \sin(\omega t)$
3. In a spring-mass system the motion of the mass is described by $$x=A_1\cos(\omega t)+A_2\sin(\omega t)$$ where $x$ is the distance of the mass from its equilibrium position, $\omega$ is the natural frequency of oscillations, and $A_1$ and $A_2$ are constants. For $A_1=1$, $A_2=\sqrt{3}$ and $\omega=10\,\text{rad s}^{-1}$:
   1. Write $x$ in the form $A\sin(\omega t+\phi)$ and state the amplitude of $x$.
   2. Sketch one complete cycle of $x$, labelling $A$, $\phi$ and the period $T$.