Exercise Set 2 Answers

These exercises cover the topics of Functions and Graphs.

  1. Sketch the graphs of the following functions on the interval \(-2\le x \le 2\).

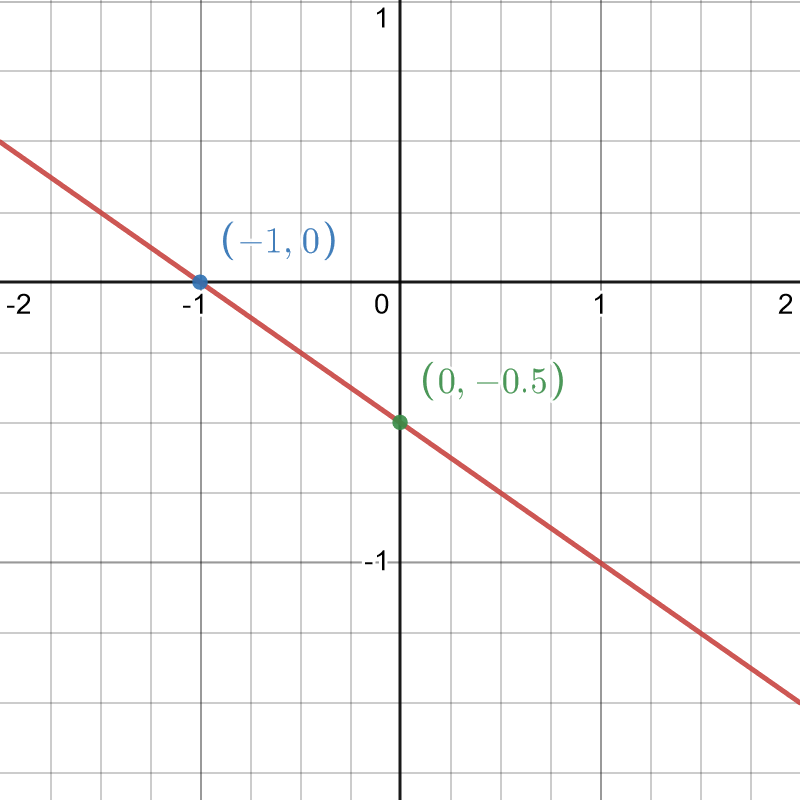
    1. \(y=-\frac{1}{2}(x+1)\)
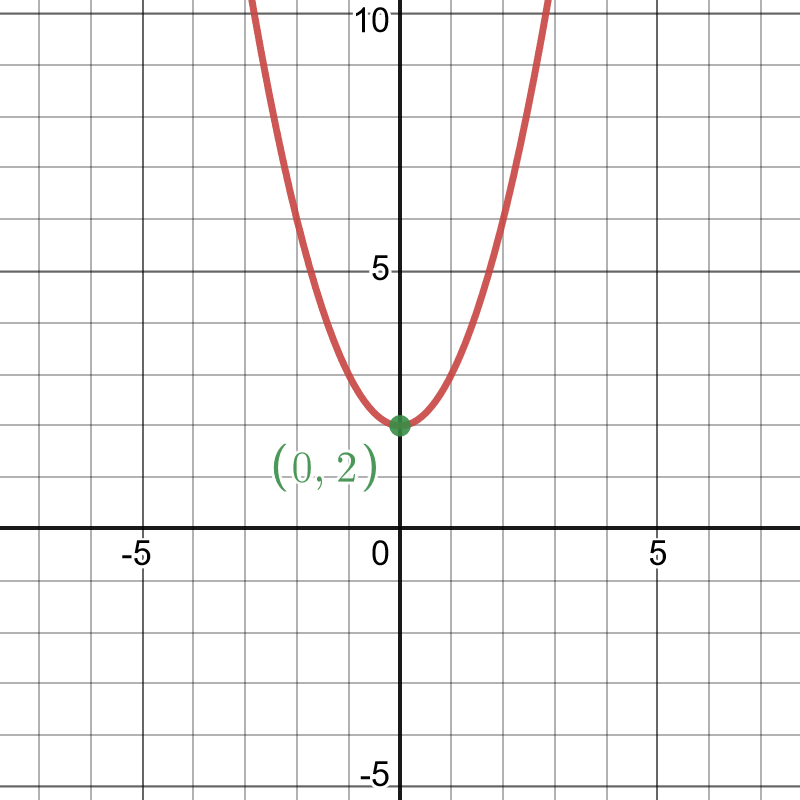
    2. \(y=x^2+2\)
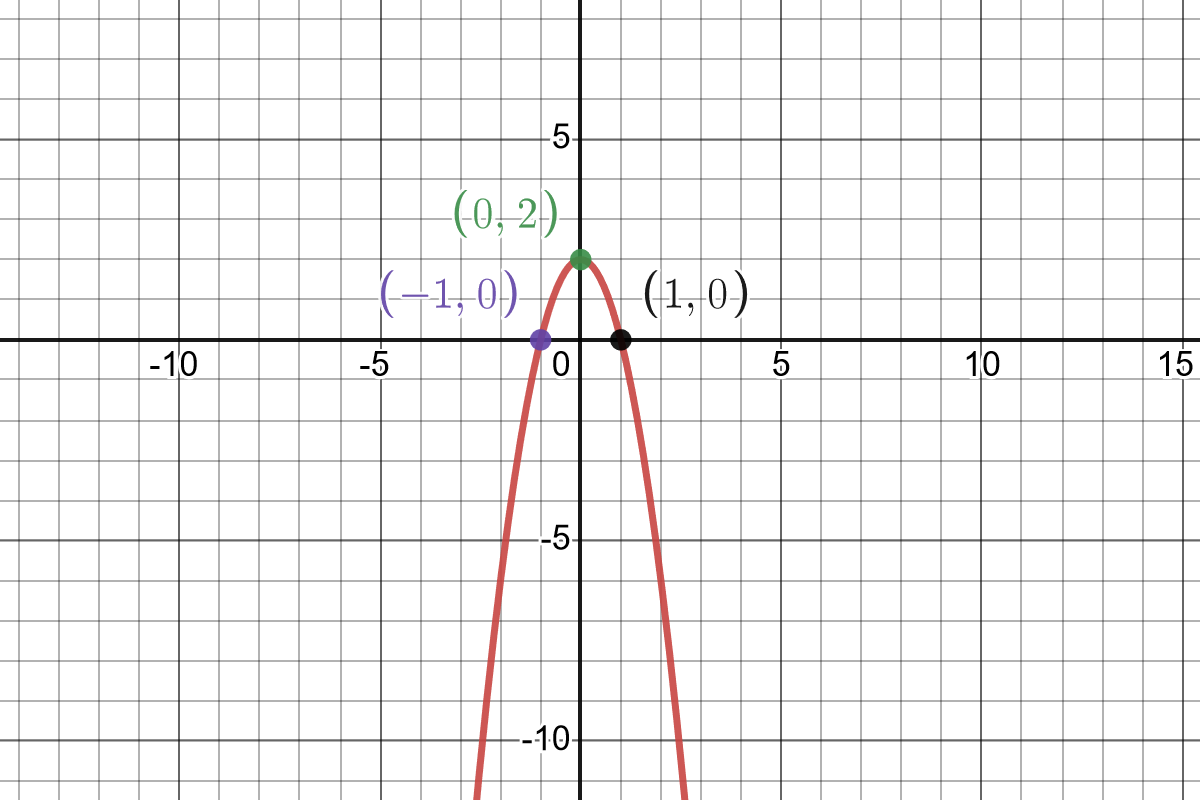
    3. \(y=-2x^2+2\)
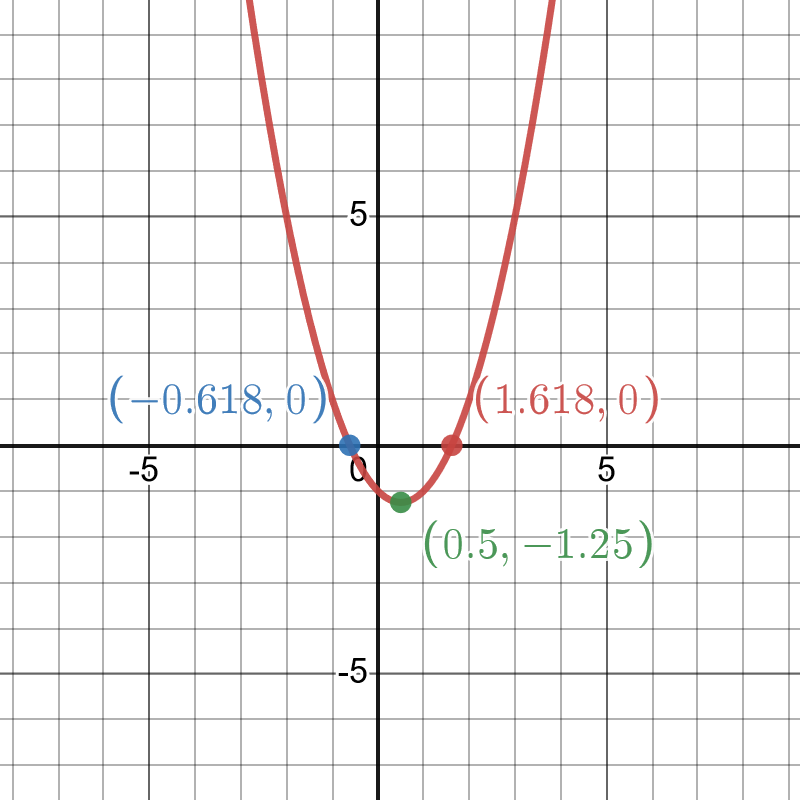
    4. \(y=x^2-x-1\)
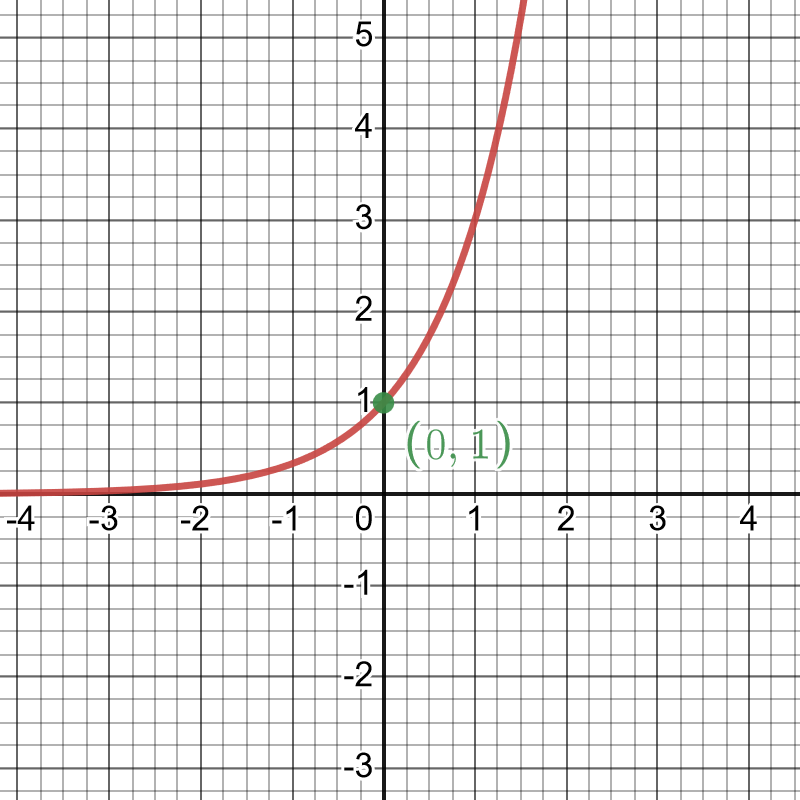
    5. \(y=3^x\)
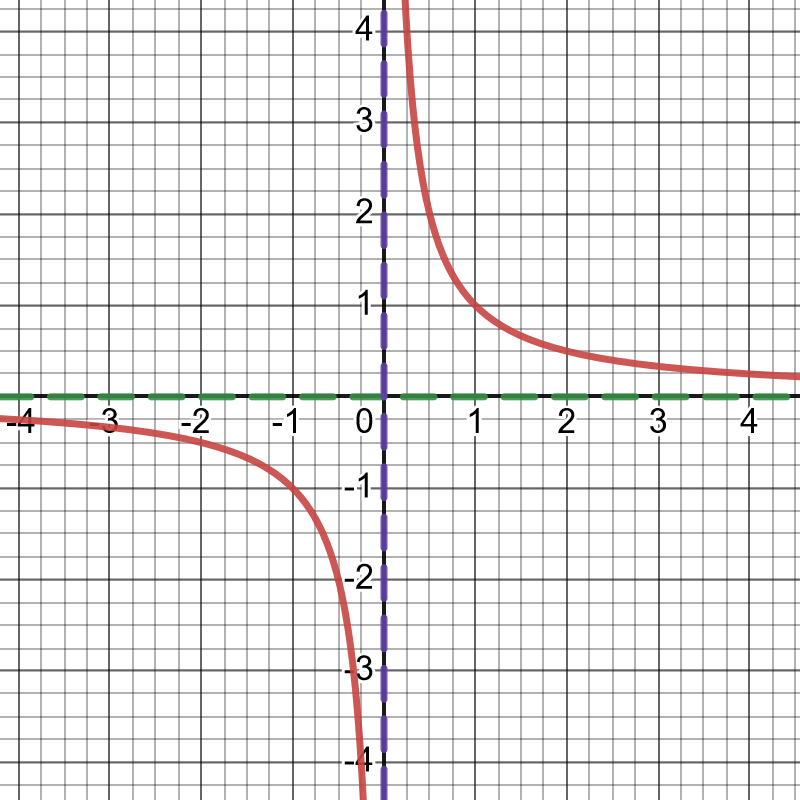
    6. \(y=\frac{1}{x}\)

    Tips: find where the functions cross the axes; use completing the square to find the maximum or minimum of quadratics; identify any asymptotes.

    Answers:

    1. Expanding: \(y=-\frac{1}{2}x-\frac{1}{2}\) which we recognise as a line with gradient \(-\frac{1}{2}\) and y intercept \(-\frac{1}{2}\). Solving for \(y=0\) gives the x intercept as \((-1,0)\).

    2. This is a parabola shifted up by 2 units.

    3. This is an “upside down” parabola, shifted up by two units.

    4. Completing the square \(y=(x-\frac{1}{2})^2-\frac{5}{4}\). Since the squared term is always non-negative, it is smallest when it is zero at \(x=\frac{1}{2}\). This is the position of the minimum, and at this point \(y=-\frac{5}{4}\). Factorising: \((x-\frac{1+\sqrt{5}}{2})(x-\frac{1-\sqrt{5}}{2})\), so the curve crosses the x axis at \(x=\frac{1+\sqrt{5}}{2}\) and \(x=\frac{1-\sqrt{5}}{2}\). Since the coefficient of \(x^2\) is positive, the parabola opens upwards.

    5. This is an exponential \(a^x\) with \(a>1\). All exponential functions cross the y axis at \(a^0=1\) and the do not cross the \(x\) axis.

    6. This is a rational function with a vertical asymptote at \(x=0\). It is small and positive for large positive values of \(x\) and it is small and negative for large negative values of \(x\): the line \(y=0\) is a horizontal asymptote.

  2. Sketch the following graphs (with \(x\) in radians):

    1. \(y=\sin(x)\)
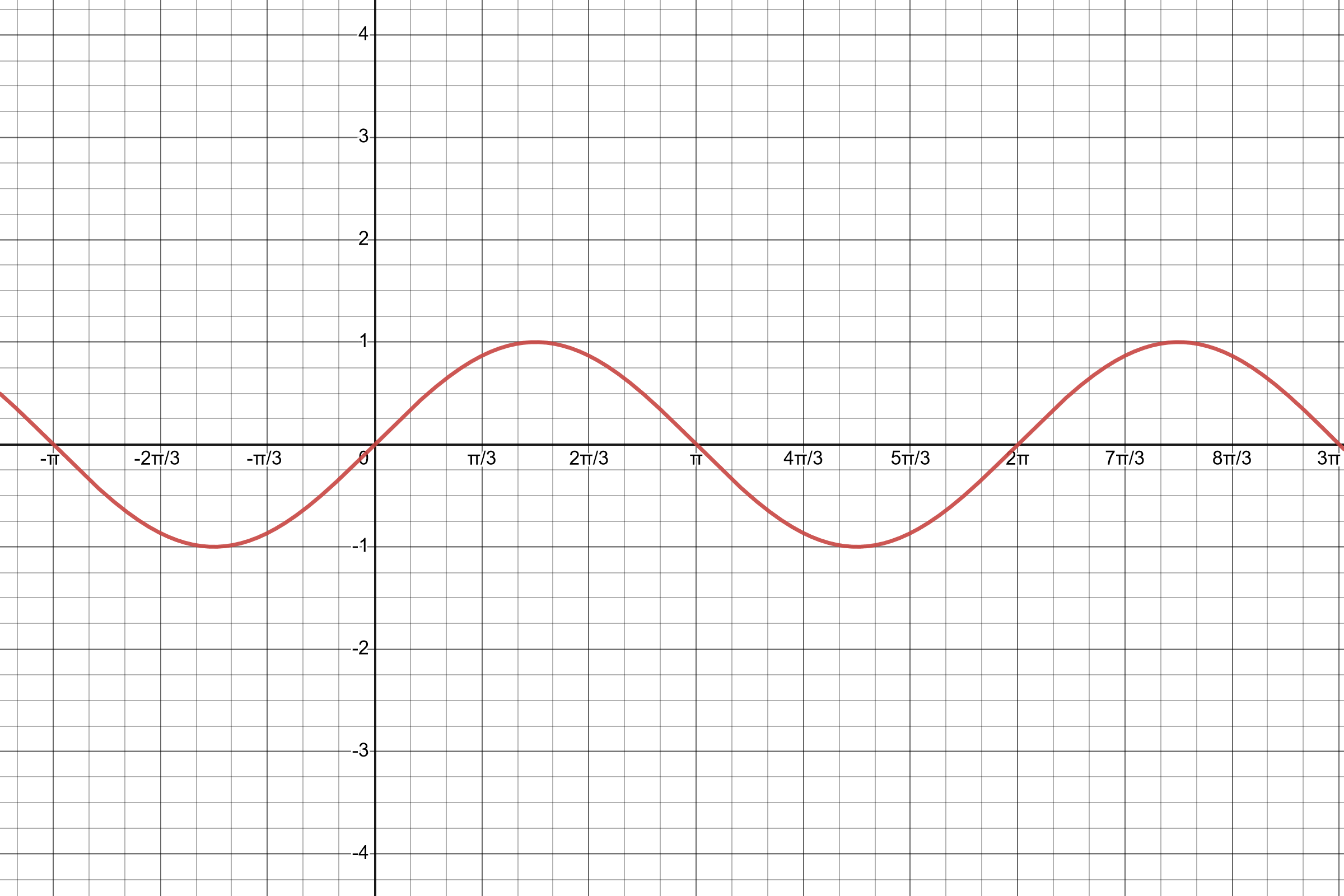
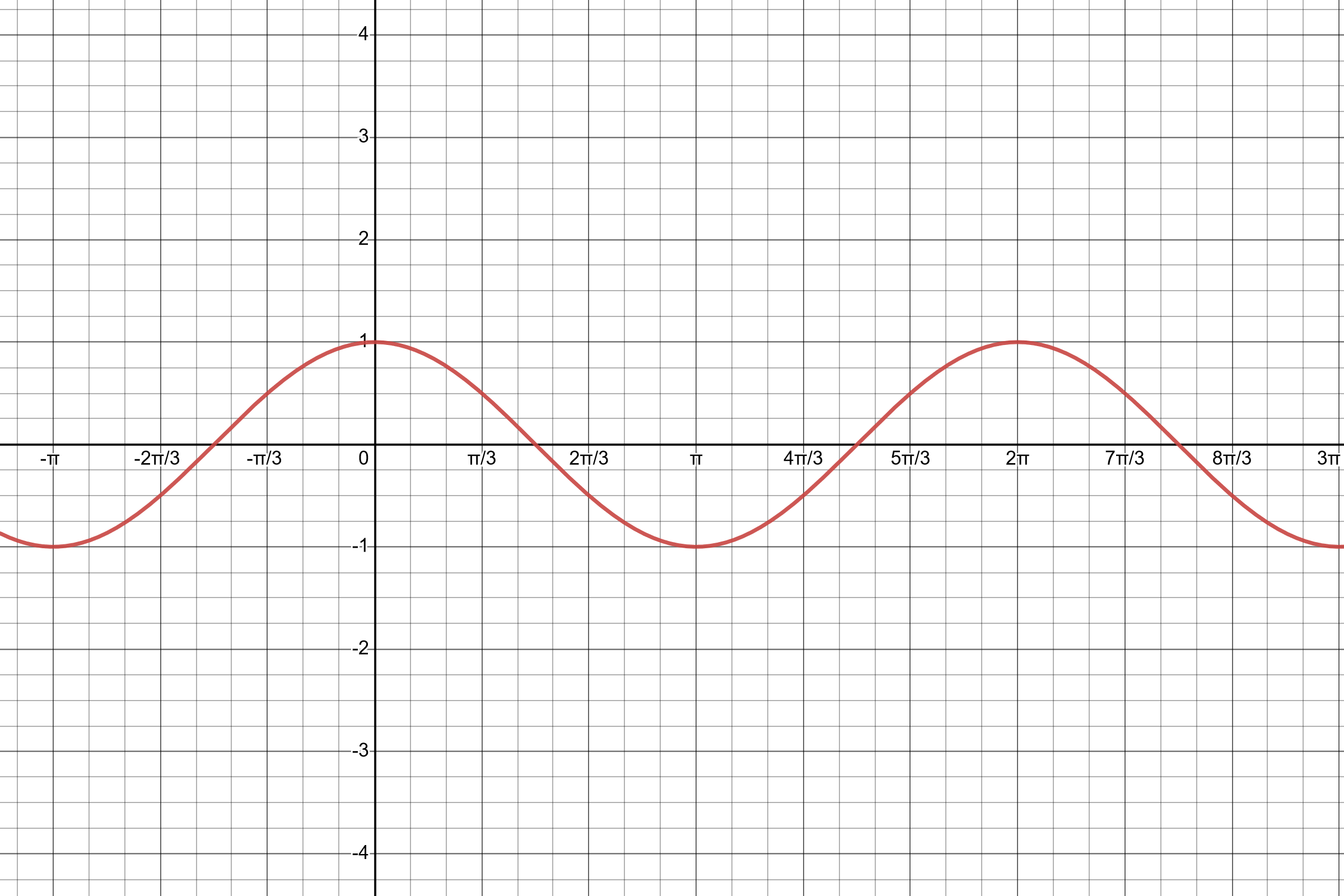
    2. \(y=\sin(x+\frac{\pi}{2})\) (does this look familiar?)
    3. \(y=\sin(2x)\)
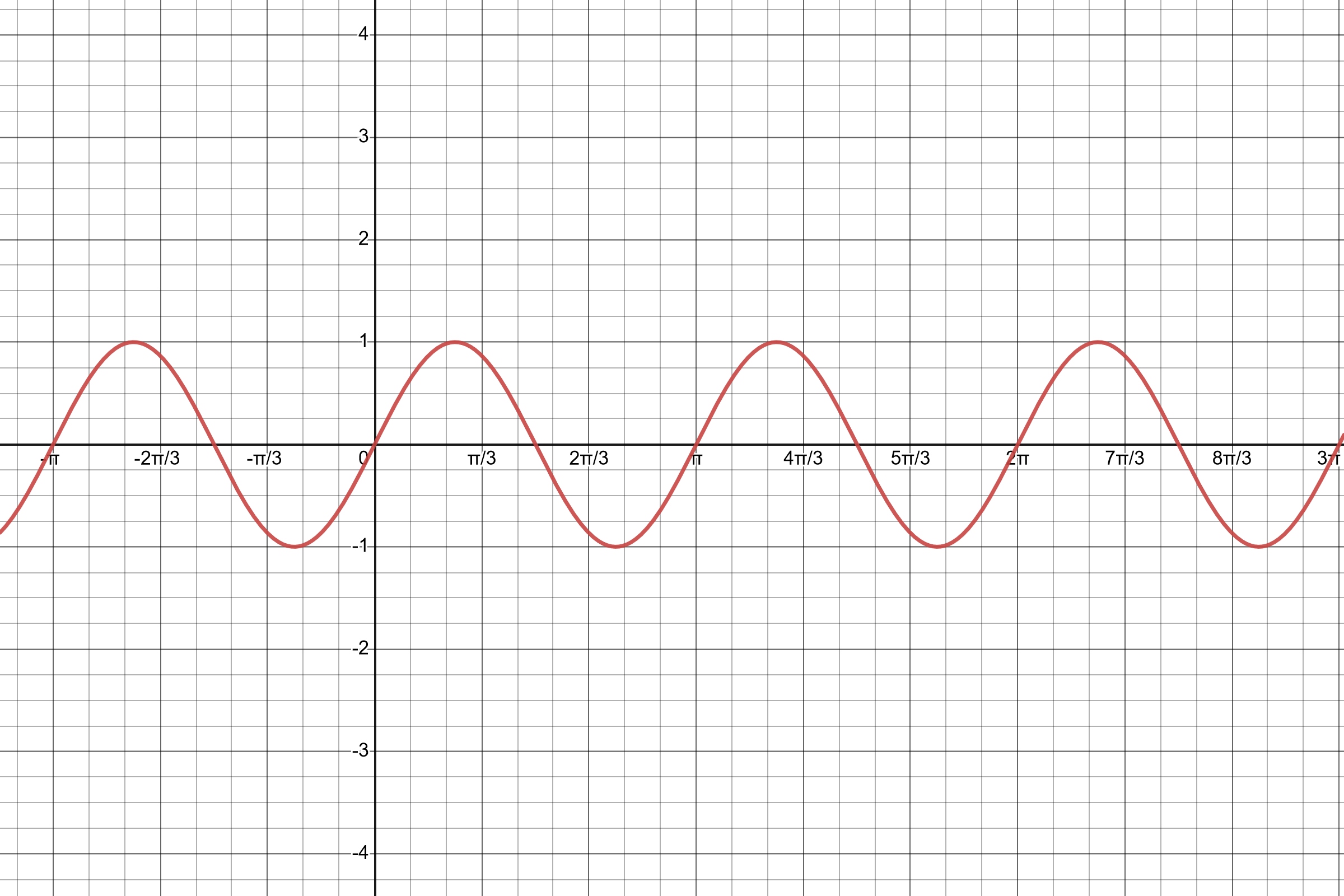
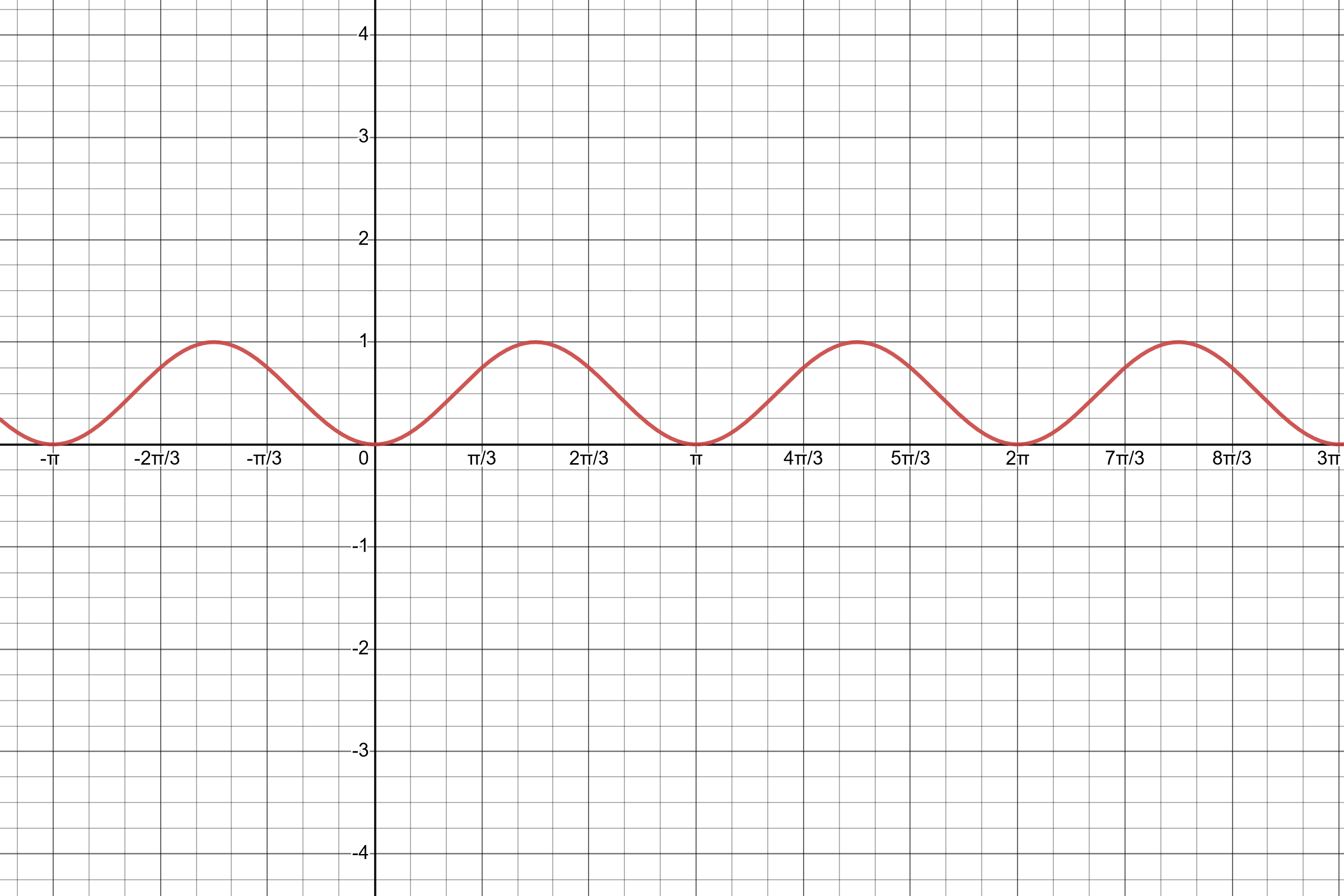
    4. \(y=\sin^2(x)\)

    Answers:

    1. You should be familiar with this graph and the location of maxima, minima and axis intercepts.

    2. Note that \(\sin(x+\frac{\pi}{2})=\cos(x)\).

    3. This is double the angular frequency of the usual sine function.

    4. Note that all the y values are non-negative.

  3. If we had the graph of a function \(f(x)\), describe what would change qualitatively for the graph of \(f(a\times x)\) where \(a\) is a constant. Consider the cases:

    1. \(a>1\)
    2. \(0 < a < 1\)
    3. \(-1 < a < 0\)
    4. \(a<-1\)

    Answers:

    1. For \(a>1\), the graph is “squeezed” along the x axis, with the value at \(x=0\) remaining unchanged.
    2. For \(0 < a <1\), the graph is expanded along the x axis, again with the value at \(x=0\) unchanged.
    3. For \(-1 < a <0\), the graph is again expanded, along the x axis, but the minus sign in \(a\) also means that the graph is reflected in the y axis.
    4. For \(a<-1\), the graph is squeezed horizontally and reflected in the y axis.

  4. If we had the graph of a function \(f(x)\), describe what would change qualitatively for the graph of \(f(x+b)\) where \(b\) is a constant. Consider the cases:

    1. \(b>0\)
    2. \(b<0\)

    Answers:

    1. For \(b>0\), the \(f(x+b)\) is the graph of \(f(x)\) translated to the left by distance \(b\)
    2. For \(b<0\), the whole graph is translated to the right by distance \(b\)

  5. If we had the graph of a function \(f(x)\), describe what would change qualitatively for the graph of \(f(x)+c\) where \(c\) is a constant. Consider the cases:

    1. \(c>0\)
    2. \(c<0\)

    Answers:

    1. For \(c>0\), \(f(x)+c\) is the graph of \(f(x)\) shifted vertically up along the y axis
    2. For \(c<0\), \(f(x)+c\) is the graph of \(f(x)\) shifted vertically down along the y axis